Vector Forces - ropebook

Vector forces become apparent whenever there is an internal angle greater than 0° between two or more rigging components or anchorage points.

For ease of explanation, a vector force is typically trying to pull horizontally as well as vertically. This has a multiplying effect on the loads that are felt at the anchor points and likewise the tension exerted within the rigging equipment, be it ropes, slings, strops or chains.

Force is an influence that has both magnitude and direction, it is usually given in the dynamic unit of Newtons (N). For ease of explanation we have used kilograms on this page.

The Basics

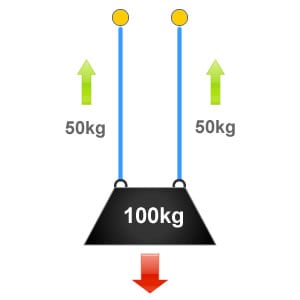
To start with the basics, if we imagine a load of 100kg suspended equally from two slings then each sling would equally share half of the loads weight.

In the situation illustrated to the right, the weight of the load = 100kg. The load is supported by two slings of equal configuration with no internal angle, so 100kg / 2 = 50kg. This means that each sling and anchor point is being subject to 50kg or 50% of the loads weight.

The Ideal Angle

As the internal angle between the rigging slings increases then additional forces (vector forces) begin to be applied to each sling / anchor point.

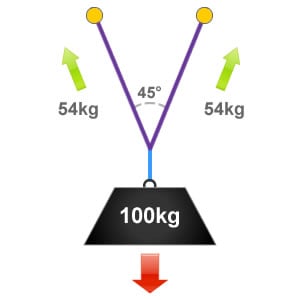
When rigging ropes the ‘ideal angle’ is approximately 45°, at the ideal angle there would be 54% of the loads weight being distributed to each anchor device. Although this is over half of the original weight of the load we have still gained an advantage by sharing it between the two anchor points.

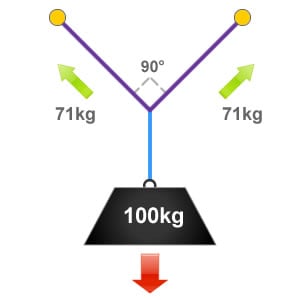
The 'OK' Angle

An internal angle of 90° between ropes and rigging components is sometimes referred to as the ‘OK’ angle. At this angle 71% of the loads weight will be distributed to each anchor component, so in this example that will be 71kg.

It is often easier to roughly estimate a 90° or right-angle when undertaking rigging tasks. By staying at or below this angle ensures that we don’t load our anchor components with excessive forces.

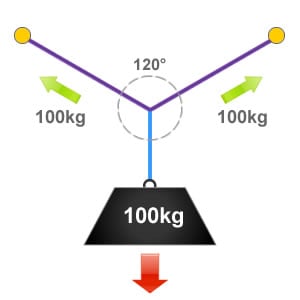
The Critical Angle

A basic way to understand the effect of vector forces is to imagine that if a full circle equates to 360° and this was split into three equal parts we would end up with three angles of 120°, as show in the illustration on the right. An internal angle of 120° is also defined as the ‘critical angle’.

Because everything is in equilibrium at the critical angle of 120°, whatever the load weighs is what we have being exerted to each anchor point and each item of rigging equipment. So in this example it is 100kg or 100% of the loads weight.

The Calculations

Vector forces can be calculated using mathematical formula. So far on this page we have used kilograms to represent the loads in the illustrations. As a kilogram is a measurement of mass, this should be converted to weight (Newtons) to calculate the resultant force correctly.

Providing that the rigging components are sharing the weight of the load equally, such as in a ‘Y’ hang then the following equation can be used:

Where:

F is the resultant force exerted to each anchorage.
w is the weight of the load.
α is the internal angle between the two slings.

Force is an influence that has both magnitude and direction, it is usually given in the dynamic unit of Newtons (N). For simplicity we have used kilograms for the examples on this page.

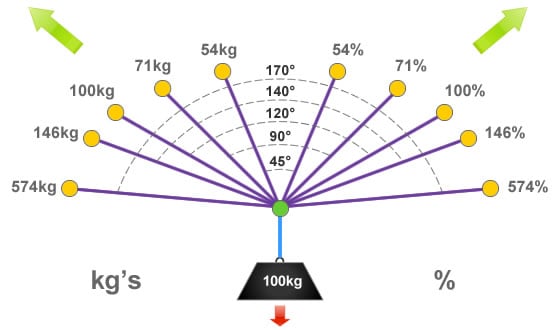
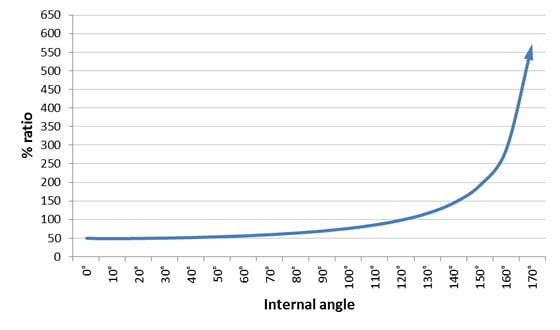
Vector Force Chart

This chart displays the resultant force applied to each anchor point / rigging component when the load is equally shared in a Y-hang rigging configuration. The ratio is also given in percentages as this is often an easier way to calculate forces relevant to the specific weight of the load.

Notice that when the critical angle of 120° is exceeded, then these forces increase dramatically. If an angle of 175° could be achieved (although this would be extremely difficult) then with a 100kg load there would nearly be 1150kg being felt by each anchor component. Something worth keeping in mind when working with Tensioned Lines, Cross Hauls and Tyrolean’s!

Using the Percentage Factor

It is not always the case that the load will weigh 100kg, it is far easier to calculate the relevant vector forces from a percentage ratio. This can be achieved by using the formula:

For example if we had a load weighing 76kg suspended from a Y-hang rigging configuration with an internal angle of 75° then:

Angle	% factor	Angle	% factor	Angle	% factor
0°	50.0	65°	59.3	130°	118.3
5°	50.1	70°	59.3	135°	130.6
10°	50.2	75°	63.0	140°	146.2
15°	50.4	80°	65.3	145°	166.8
20°	50.8	85°	67.8	150°	193.2
25°	51.2	90°	70.7	155°	231.0
30°	51.8	95°	74.0	160°	287.9
35°	52.4	100°	77.8	165°	383.1
40°	53.2	105°	82.1	170°	573.7
45°	54.1	110°	87.2	175°	1146.9
50°	55.2	115°	93.1	180°	∞
55°	56.4	120°	100.0
60°	57.7	125°	108.9

Vector Force Graph

The graph below displays the relationship between the internal angle and the percentage ratio. At 180° this line would continue to rise vertically, meaning that from a mathematical point of view the force exerted on each anchor point would be infinite.

Problem One-Eighty

What would happen if we could actually achieve an internal angle of 180°? Although this would be physically impossible as the rope or slings would even deflect under their own weight, a perfect internal angle of 180° would produce an infinite amount of force exerted to the rigging components and anchor points.

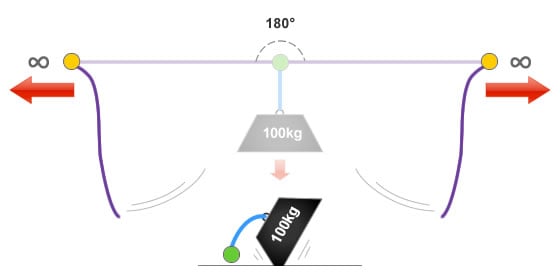
The reason for this is that in trying to calculate the forces using the equation would result in a number being divided by 0. It is impossible to divide a number by zero, try this on a calculator and an E or error message will be displayed.

Where else are Vector Forces found?

These additional vector forces will also occur wherever internal angles between rigging equipment and loads are apparent. In addition to rigging Y-hangs, this will also include;