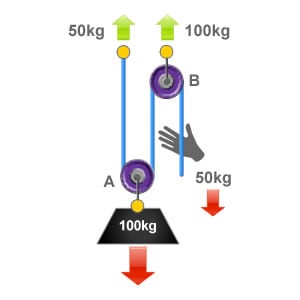
Angular Vector Forces
Angular vector forces occur when ropes are passed through a deviation or a directional pulley. Dependent on the angle created, this can have a multiplying effect on the forces that are felt at the deviation or directional pulley components and the associated anchor points.
Force is an influence that has both magnitude and direction, it is usually given in the dynamic unit of Newtons (N). For ease of explanation we have used kilograms on this page.
The Basics
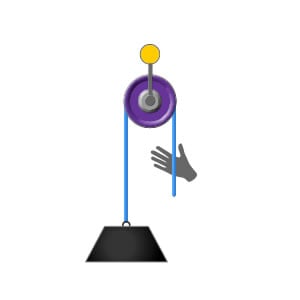
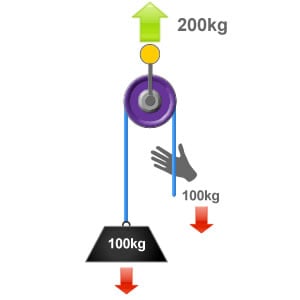
Here we have a load weighing 100kg. A rope has been attached to the load and then passed through a directional pulley which returns the rope back down to the user at ground level. The two sections of rope are in parallel with each other so there is no internal or included angle.
In this situation the directional pulley and its anchor point are actually being loaded with 200kg, as there is the weight of the load on one side and a effort of 100kg is being applied by the user on the other to hold the load in place.
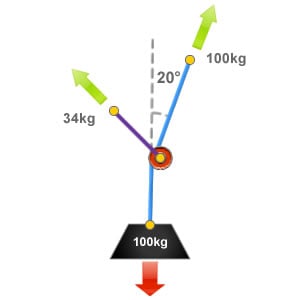
Deflection Angle of 20°
Here the rope has been deviated away from its original line (in this illustration the vertical) by 20°. While all of the weight of the load is being exerted to the main anchor point, a percentage of the loads weight is also being applied to the deviation / directional pulley components.
With a deviation of 20°, there will be 34% of the loads weight being applied to the deviation / directional pulley anchor point. In this situation, where we have a 100kg load this would produce a force of 34kg on the deviation / directional pulley.
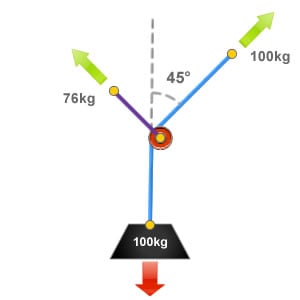
Deflection Angle of 45°
As the angle of deflection increases then the force exerted on the deviation or directional pulley anchor also increases. An angle of deflection measuring 45° would produce a force on the deviation anchor point equivalent to 76% of the loads weight, so in this example where the load weighs 100kg that would be 76kg.
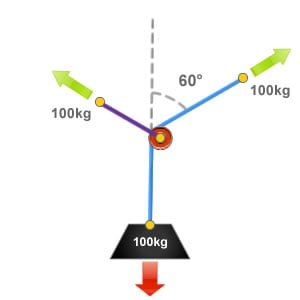
Deflection Angle of 60°
With an angle of deflection measuring 60°, 100% of the loads weight will be applied to the deviation or directional pulley anchor point.
This can be compared to the critical angle found in vector forces when rigging y hangs, as all three angles are equal.
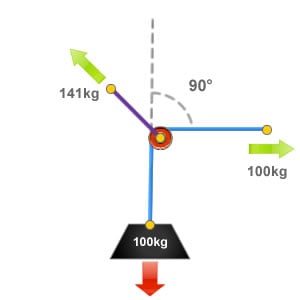
Deflection Angle of 90°
A 90° angle of deflection results in a force equal to 141% of the loads weight being applied to the deviation or directional pulley anchor point.
Note that this would also be the same loading for an included angle of 90° as they are both the same.
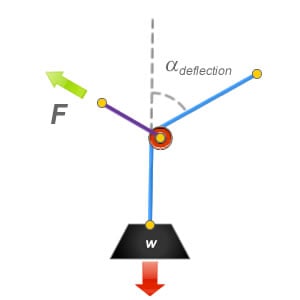
Deflection Angle: The Calculations
Angular Vector forces can be calculated using mathematical formula. Here is a formula that we can use to calculate the amount of force that is being applied to the deviation or directional pulley anchor point when measuring from the angle of deflection.
So far on this page we have used kilograms to represent the loads in the illustrations. As a kilogram is a measurement of mass, this should be converted to weight (Newtons) to calculate the resultant force correctly.

Where:
F is the resultant force exerted to the deviation or directional pulley anchor point.
w is the weight of the load.
α is the angle that the rope has been deflected away from its original line.
Deflection Angle: Using the Percentage Factor
The percentage factor can be used to calculate the amount of force that is being applied to the deviation or directional pulley anchor point. This can be achieved by using the following formula:
![]()
| Angle | % factor | Angle | % factor | Angle | % factor |
|---|---|---|---|---|---|
| 0° | 0.0 | 65° | 107.5 | 130° | 181.3 |
| 5° | 8.7 | 70° | 114.7 | 135° | 184.8 |
| 10° | 17.4 | 75° | 121.7 | 140° | 187.9 |
| 15° | 26.1 | 80° | 128.6 | 145° | 190.7 |
| 20° | 34.7 | 85° | 135.1 | 150° | 193.2 |
| 25° | 43.3 | 90° | 141.4 | 155° | 195.3 |
| 30° | 51.8 | 95° | 147.4 | 160° | 197.0 |
| 35° | 60.1 | 100° | 153.2 | 165° | 198.3 |
| 40° | 68.4 | 105° | 158.7 | 170° | 199.2 |
| 45° | 76.5 | 110° | 163.8 | 175° | 199.8 |
| 50° | 84.5 | 115° | 168.8 | 180° | 200.0 |
| 55° | 92.3 | 120° | 173.2 | ||
| 60° | 100.0 | 125° | 177.4 |
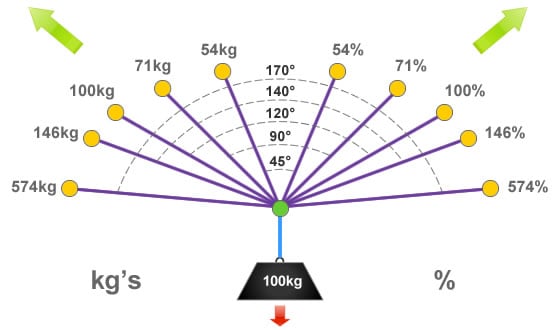
Looking at it from a different angle
We can measure the angle of a deviation or directional pulley in two different ways, which ever is easiest and more relevant to the specific set-up. Here we have detailed both methods; measuring from the angle of deflection and measuring from the included angle.
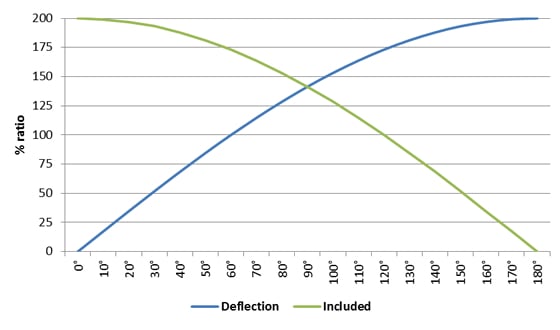
An angle of deflection is a measurement of how many degrees the rope has been deviated or diverted away from its original line. These angles will be easier to estimate when using small deviations.
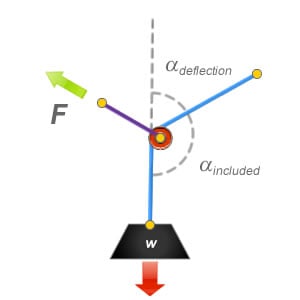
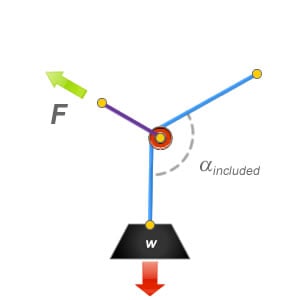
The included angle is measured between the section of rope that passes through the deviation or directional pulley. It is usually easier to calculate this type of angular vector force when using pulley systems and high re-directs.
When measuring either deviations or directional pulleys, both the included angle and the angle of deflection should always result in 180° when added together.
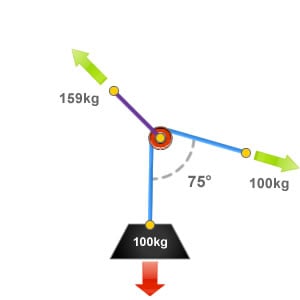
Included Angle of 75°
In this situation we have measured the included angle between the section of rope which passes around the pulley.
The included angle is 75°, this would produce a force on the directional pulley or deviation equivalent to 159% of the loads weight. So in this example that is 159kg!
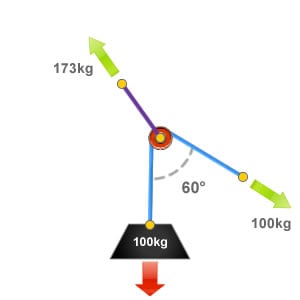
Included Angle of 60°
Again we have measured the included angle formed where the rope passes through the directional pulley or deviation.
With an included angle of 60°, a force equivalent to 173% of the loads weight will be applied to the directional pulley or deviation.
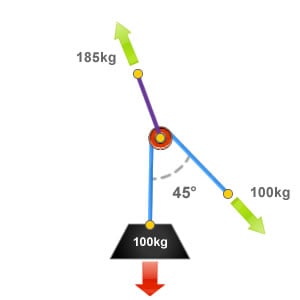
Included Angle of 45°
In this illustration the included angle measures 45°. As the included angle created by the rope passing through the pulley or deviation decreases towards 0° the force applied to the directional pulley or deviation increases.
In this example the force applied will be roughly equal 185% of the loads weight.
Included Angle: The Calculations
Angular Vector forces can be calculated using mathematical formula. Here is a formula that we can use to calculate the amount of force that is being applied to the deviation or directional pulley anchor point when measuring from the included angle.
So far on this page we have used kilograms to represent the loads in the illustrations. As a kilogram is a measurement of mass, this should be converted to weight (Newtons) to calculate the resultant force correctly.

Where:
F is the resultant force exerted to the deviation or directional pulley anchor point.
w is the weight of the load.
α is the angle that the rope has been deflected away from its original line.
Included Angle: Using the Percentage Factor
The percentage factor can be used to calculate the amount of force that is being applied to the deviation / directional pulley anchor point. This can be achieved by using the following formula:
![]()
| Angle | % factor | Angle | % factor | Angle | % factor |
|---|---|---|---|---|---|
| 0° | 200.0 | 65° | 168.8 | 130° | 84.5 |
| 5° | 199.8 | 70° | 163.8 | 135° | 76.5 |
| 10° | 199.2 | 75° | 158.7 | 140° | 68.4 |
| 15° | 198.3 | 80° | 153.2 | 145° | 60.1 |
| 20° | 197.0 | 85° | 147.4 | 150° | 51.8 |
| 25° | 195.3 | 90° | 141.4 | 155° | 43.3 |
| 30° | 193.2 | 95° | 135.1 | 160° | 34.7 |
| 35° | 190.7 | 100° | 128.6 | 165° | 26.1 |
| 40° | 187.9 | 105° | 121.7 | 170° | 17.4 |
| 45° | 184.8 | 110° | 114.7 | 175° | 8.7 |
| 50° | 181.3 | 115° | 107.5 | 180° | 0.0 |
| 55° | 177.4 | 120° | 100.0 | ||
| 60° | 173.2 | 125° | 92.3 |
Included Angle: Using the Percentage Factor
The graph below displays the force applied to the deviation or directional pulley anchor point in comparison to the relationship between the deflection angle and the included angle.